阶乘后的零

一、介绍

此题出自力扣网题库第172题，我刚开始没有想到，后面看了题解才明白的。

先看看题目，讲得很简单

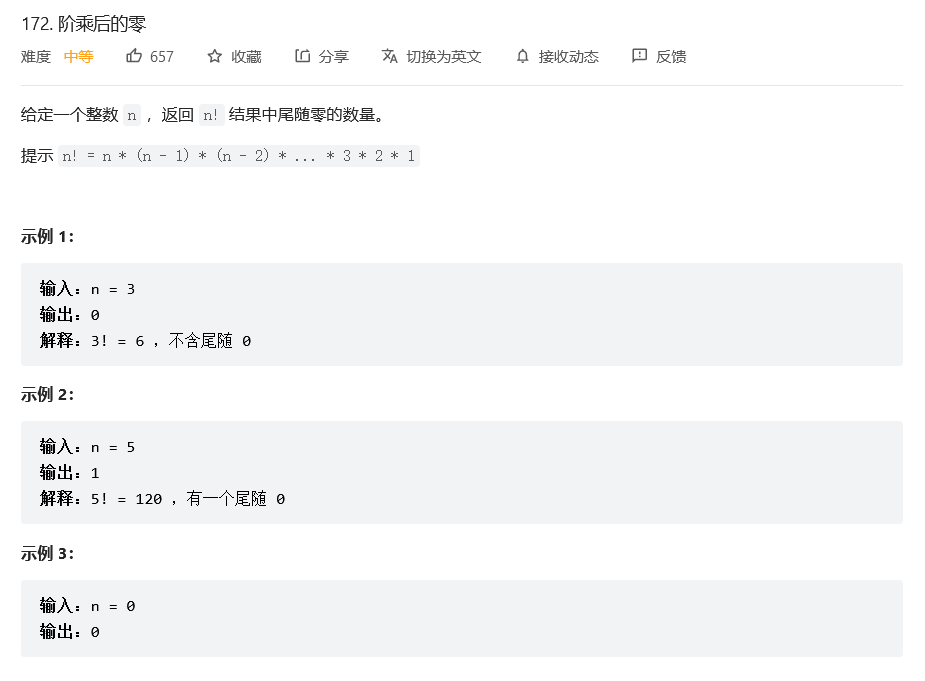
image-20220326174614333

还有入参的限制，0 <= n <= 104

1
2
3
4
5
class Solution {
    public int trailingZeroes(int n) {
		// TODO ...
    }
}

放一个计算器，一会自己可以看看规律

输入数字n：
结果：1

二、解题思路

1）暴力破解

暴力破解，算出答案，再转字符串，计算出末尾零的个数。

这种方法想都不要想，这可是阶乘，数字量很大的，很容易溢出。不然上面用计算器来试试。

2）优化

不知道你用计算器试过了没有，也不知道你有没有得到规律，我们先一步一步来分析

  1. 首先要看这道题想要的结果是什么，是零的个数

  2. 再看题目，阶乘阶乘，里面都是乘法计算，所以想要得到零，必须要乘上10，那么这个10就是因子

  3. 思路到这，第一步就清除了，查询n中有多少个10或者10的倍数，就有多少个零

然而，当你用计算器去试了一下，结果发现，5!=1205! = 120，这也有一个零

  1. 思维再次扩展，可以发现5*偶数=10的倍数的，这样一来因子是5，而不是10

  2. 由于偶数很多，所以我们只需要计算出n中有多少个5的倍数这样的数，就可以正确得到答案了

1
2
3
4
public int trailingZeroes(int n) {
    int count = n / 5;
    return count;
}

思维发散至这里，已经很强了，但还不够！！！因为25!=1551121004333098598400000025! = 15511210043330985984000000，足足有6个0，这是为什么？？？

  1. 如果只是遍历5的倍数，算出总共有多少5因子的倍数的话，还是不够的

  2. 但要注意25这个数，是由5*5而来，要多算一个零。同理125，是由5 * 5 * 5 而来，再多算一个零

  3. 按照步骤2，我们需要 (n/5) + (n/25) + (n/125) + … ​

  4. 可以对步骤3的公式进行优化，提取出n/5n/5，来进行计算，直到n小于5为止，所以就得到了下面这个答案

1
2
3
4
5
6
7
8
9
10
class Solution {
    public int trailingZeroes(int n) {
        int count = 0;
        while(n >= 5) {
            count += n / 5;
            n /= 5;
        }
        return count;
    }
}

三、最后

这道题，我拿到确实懵逼了，直到看完题解才恍然大悟，只能大声高呼，牛逼。

我是半月，祝你幸福！！！