排序算法之堆排序

一、介绍

由于堆排序与以前的排序都不太一样，他是基于顺序存储的二叉树结构来进行的排序，故此拉出来单独做了一张。

以前的排序算法传送门

二、概念

在开始编码之前，我们先要理解下面两个概念

1）顺序存储的二叉树

对于任意一个数组，它都可以转换为一个完全二叉树

如下图，平铺着转换就可以了

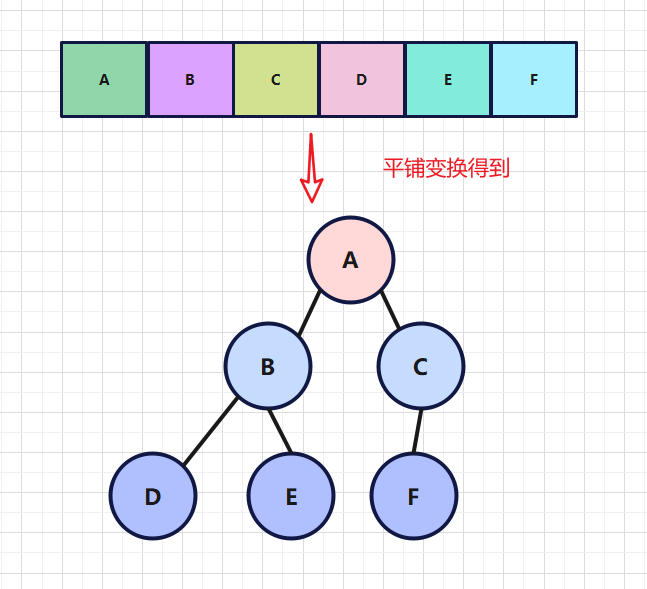
对于一个顺序存储的二叉树，它的节点连接定义如下

下标N的左节点： $2n+1$

下标N的右节点： $2n+2$

下标N的父节点： $\frac{n-1}{2}$

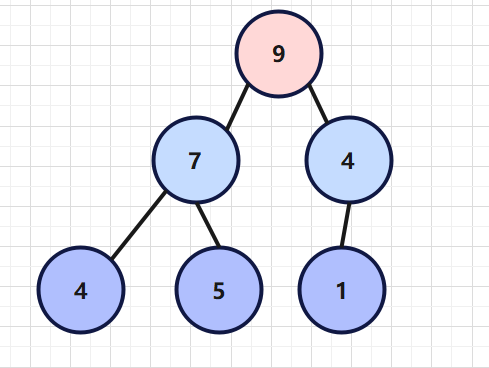
2）大小顶堆

什么是大顶堆，就是父节点永远都比子节点的数要大，故名为大顶堆。如下图

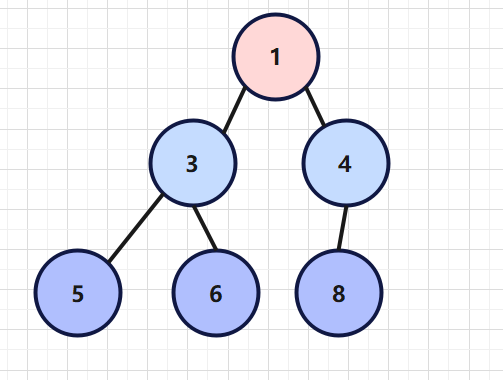
相反，如果一颗二叉树的父节点都比子节点的数要小，那么它就是小顶堆。如下图

三、代码

简单的来说，堆排序就是将持续的将，一个顺序存储的二叉树变成大顶堆或者小顶堆。

升序使用大顶堆，降序使用小顶堆。

步骤如下，这是第一步

从非叶子节点开始前遍历
每一个非叶子节点，都将和自己的左节点、右节点进行判断
根据大小顶堆的需要，来进行替换
直到称为一个大小顶堆

成为了大小顶堆之后，我们将得到了一个最大或者最小的数，也就是大小顶堆根节点的数

将这个根节点与最后的叶子节点进行替换，也就是将最大或者最小的数放到了最后

找到了一个数还不够，我们将重复上面的步骤

重复第一步，但不要影响放到最后的数
得到大小顶堆的根节点后，进行替换，不是和最后的数进行替换了，而是依次往前替换。
直到排序玩成

代码如下

package com.banmoon.algorithm.order;

import java.util.Arrays;

/**
 * 堆排序
 */
public class Demo08 {

    public static void main(String[] args) {
//        int[] arr = {128, 359, 26, 78, 98, 5, 789, 12, 6, 2};
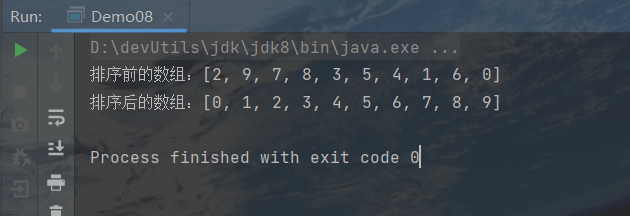
        int[] arr = {2, 9, 7, 8, 3, 5, 4, 1, 6, 0};
        System.out.println("排序前的数组：" + Arrays.toString(arr));
        int[] sortArr = sort(arr);
        System.out.println("排序后的数组：" + Arrays.toString(sortArr));
    }

    private static int[] sort(int[] arr) {
        // 先进行一次大顶推的转换
        int last = (arr.length - 1) / 2;
        for (int i = last; i >= 0; i--) {
            maxHeap(arr, arr.length, i);
        }
        // 将这个根节点与最后的叶子节点进行替换，也就是将最大的数放到了最后
        for (int i = arr.length-1; i > 0; i--) {
            // 替换最前和最后的数
            int temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;
            // 替换后，需要将根节点的数进行一次转移，重新变为大顶堆
            maxHeap(arr, i, 0);
        }
        return arr;
    }


    public static void maxHeap(int[] arr, int size, int index){
        // 左节点
        int leftIndex = index*2+1;
        // 右节点
        int rightIndex = index*2+2;
        // 和左右节点进行对比
        int max = index;;
        if(leftIndex < size && arr[leftIndex] > arr[max])
            max = leftIndex;
        if(rightIndex < size && arr[rightIndex] > arr[max])
            max = rightIndex;
        // 进行交换
        if (max != index) {
            int temp = arr[max];
            arr[max] = arr[index];
            arr[index] = temp;
            // 交换位置后，需要再对替换的index向下判断
            maxHeap(arr, size, max);
        }
    }

}