二叉树详解

一、开始

什么是树，什么又是二叉树？我知道大家都听过，但对于具体的概念，应该还是比较模糊的吧？

一起来看看，什么是树，什么又是二叉树！

二、概念

1）树结构概念

树是一种数据结构，它是由节点相连，带来的一个层次结构的数据集合，且除了根节点以外，其余节点有且只有一个父节点。

与链表不同的是，树的连接关系往往是一对多的关系。

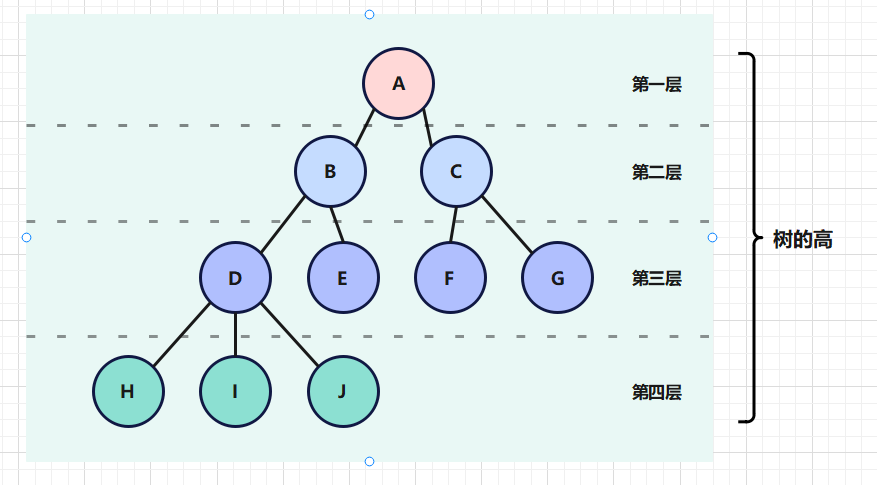
树结构通常表现为下图方式

image-20220908114633480

  • 子节点：一个节点指向下一个节点时，下个节点是上个节点的子节点。上图A节点的子节点是B节点和C节点

  • 父节点、双亲节点：一个节点指向下一个节点时，下个节点是上个节点的子节点。上图B节点的父节点是A节点

  • 兄弟节点：拥有同一个父节点的两个节点，互为兄弟节点。上图如D节点和E节点互为兄弟节点

  • 节点的度：拥有子节点的数量称为节点的度。如D节点的度为3，C节点的度为2

  • 节点的权：代表节点中存的对象。如D节点代表存了D字符

  • 根节点：一颗树最开始的节点，被称为根节点。上图为A节点

  • 叶子节点：没有子节点的节点，也就是度为0的节点。上图为H节点、E节点、F节点等

  • 内部节点、枝节点：除了根节点和叶子节点以外的节点。如B节点、C节点、D节点

  • 子树：将一颗树进行拆分，将内部节点视为根节点产生了树，称为子树。

  • 路径：从根节点到目标节点，所经过的节点路径。如D节点的路径为==A-B-D==

  • 层：由根节点为第一层，来计算节点的层。如B节点的层是2，D节点是3

  • 高度：代表当前数最大一层的节点是多少。上面这颗树的高度为4

2）二叉树

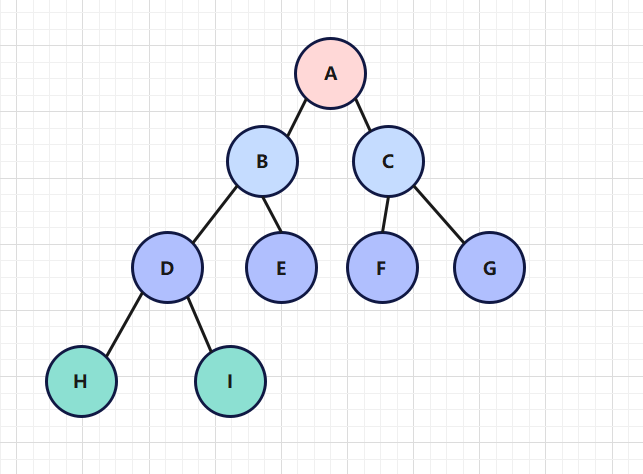
当一颗树的所有节点，它的子节点都不超过2个时，这颗树被称为二叉树。

如下图

image-20220908140252280

通过左右习惯分节点为，左节点和右节点，如B节点和C节点互为左右节点，B节点是左节点，C节点是右节点。

3）满二叉树

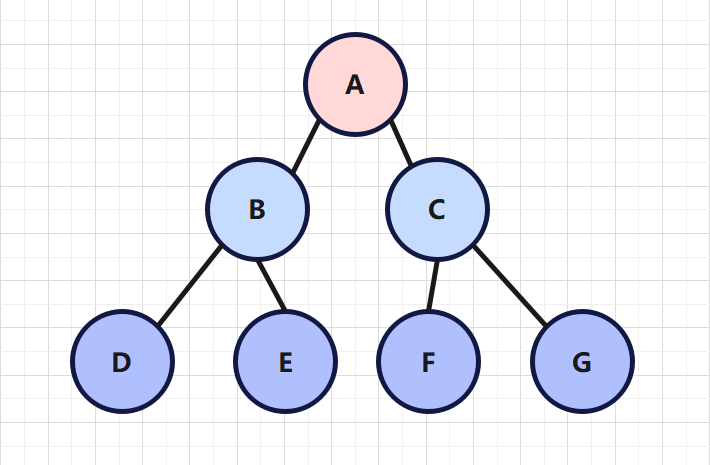
满二叉树，就是在二叉树的基础上，新增了这么一条规则。

所有叶子节点都在最后一层，且节点的总数**2n−12^n-1**，n是树的高度

如下图

image-20220918104339214

4）完全二叉树

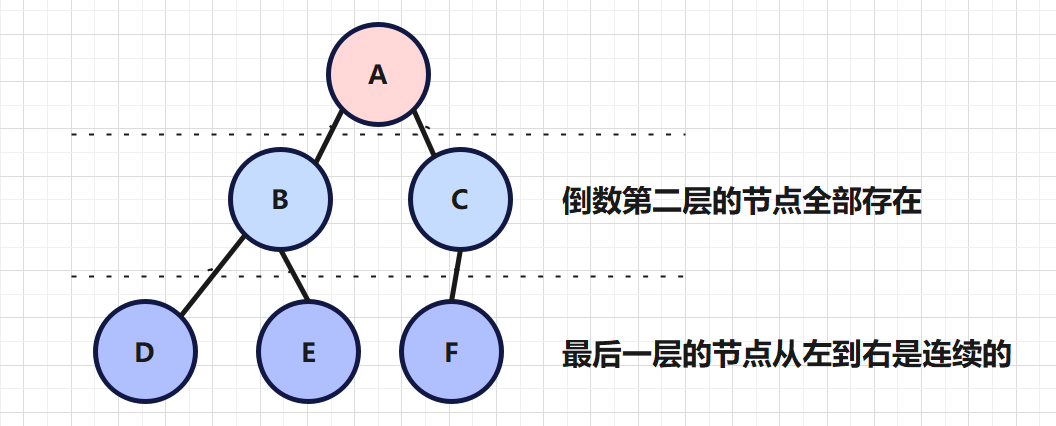
完全二叉树，就是在二叉树的基础上，新增了这么一条规则

最后一层的叶子节点，从左往右是连续的，倒数第二层的叶子节点是全部存在的。

如下图

image-20220918105053062

直观来讲，就是说，只要是满二叉树，它就一定是完全二叉树。满二叉树，只要去掉最后一层的最后几个，就是完全二叉树了。

5）二叉树的其他形态

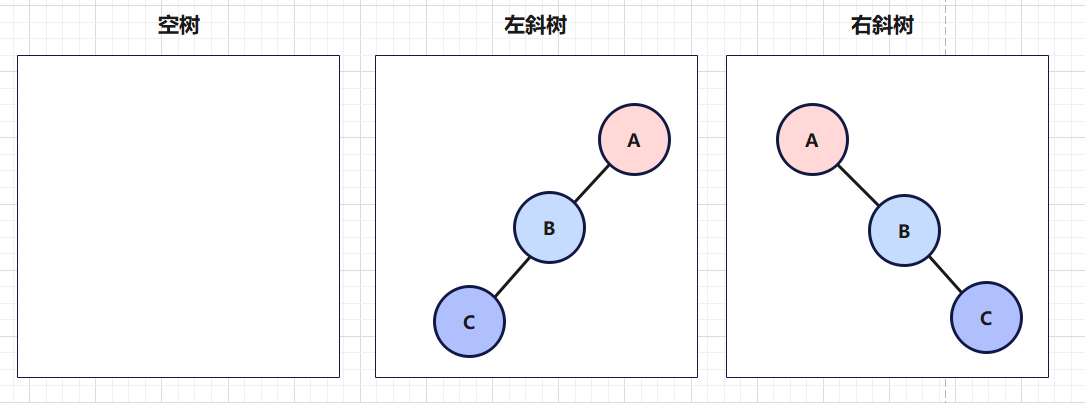
如下图

  • 空树：当一颗树中连根节点都没有时，这棵树被称为空树

  • 左斜树：当一颗树中只有左节点时，这棵树被称为左斜树

  • 右斜树：当一颗树中只有右节点时，这棵树被称为右斜树

image-20220918190230506

左斜树和右斜树本质上没有区别，它由二叉树的概念退化成为了链表。

在日常中，我们应当极力避免此种数据结构的产生。

三、代码实现

1）链式存储的二叉树

1.1）创建

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
package com.banmoon.datastructure;

import lombok.AllArgsConstructor;
import lombok.Data;
import lombok.NoArgsConstructor;

@Data
@NoArgsConstructor
@AllArgsConstructor
public class BinaryTree {

    /**
     * 根节点
     */
    private TreeNode root;

    public BinaryTree(Integer value) {
        this.root = new TreeNode(value);
    }

    @Data
    @NoArgsConstructor
    public static class TreeNode {

        /**
         * 节点值
         */
        private Integer value;

        /**
         * 左节点
         */
        private TreeNode leftNode;

        /**
         * 右节点
         */
        private TreeNode rightNode;

        public TreeNode(Integer value) {
            this.value = value;
        }
    }

}

测试如何使用这个二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
package com.banmoon.datastructure;

public class BinaryTreeTest {

    public static void main(String[] args) {
        // 创建一个空树
        BinaryTree tree = new BinaryTree();
        // 创建根节点
        BinaryTree.TreeNode node = new BinaryTree.TreeNode(1);
        tree.setRoot(node);
        // 设置左节点
        BinaryTree.TreeNode leftNode = new BinaryTree.TreeNode(2);
        node.setLeftNode(leftNode);
        // 设置右节点
        BinaryTree.TreeNode rightNode = new BinaryTree.TreeNode(3);
        node.setLeftNode(rightNode);
    }
}

1.2）遍历

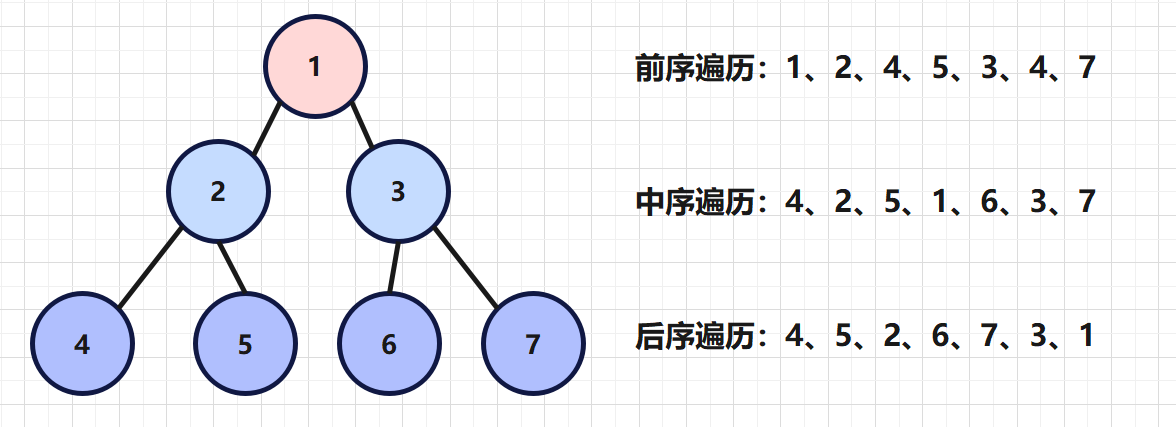
对于二叉树的遍历，我们通常可以有以下这三种情况。

  • 前序遍历：将通过根节点、左节点、右节点的顺序进行递归遍历

  • 中序遍历：将通过左节点、根节点、右节点的顺序进行递归遍历

  • 后序遍历：将通过左节点、右节点、根节点的顺序进行递归遍历

如下图

image-20220918191548399

简单的来说，就是看遍历时根节点的位置，来确定是哪种遍历方式。

接下来就写一下，三种遍历的代码吧，采用递归的方式来完成

前序遍历，frontShow()

中序遍历，middleShow()

后序遍历，backShow()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
package com.banmoon.datastructure;

import lombok.AllArgsConstructor;
import lombok.Data;
import lombok.NoArgsConstructor;

import java.util.Objects;

@Data
@NoArgsConstructor
@AllArgsConstructor
public class BinaryTree {

    /**
     * 根节点
     */
    private TreeNode root;

    public BinaryTree(Integer value) {
        this.root = new TreeNode(value);
    }

    /**
     * 前序遍历
     */
    public void frontShow() {
        if (Objects.nonNull(root))
            root.frontShow();
    }

    /**
     * 后序遍历
     */
    public void middleShow() {
        if (Objects.nonNull(root))
            root.middleShow();
    }

    /**
     * 后序遍历
     */
    public void backShow() {
        if (Objects.nonNull(root))
            root.backShow();
    }

    @Data
    @NoArgsConstructor
    public static class TreeNode {

        /**
         * 节点值
         */
        private Integer value;

        /**
         * 左节点
         */
        private TreeNode leftNode;

        /**
         * 右节点
         */
        private TreeNode rightNode;

        public TreeNode(Integer value) {
            this.value = value;
        }

        /**
         * 前序遍历
         */
        public void frontShow() {
            System.out.print(this.value);
            if (Objects.nonNull(this.leftNode))
                this.leftNode.frontShow();
            if (Objects.nonNull(this.rightNode))
                this.rightNode.frontShow();
        }

        /**
         * 中序遍历
         */
        public void middleShow() {
            if (Objects.nonNull(this.leftNode))
                this.leftNode.middleShow();
            System.out.print(this.value);
            if (Objects.nonNull(this.rightNode))
                this.rightNode.middleShow();
        }

        /**
         * 后序遍历
         */
        public void backShow() {
            if (Objects.nonNull(this.leftNode))
                this.leftNode.backShow();
            if (Objects.nonNull(this.rightNode))
                this.rightNode.backShow();
            System.out.print(this.value);
        }
    }

}

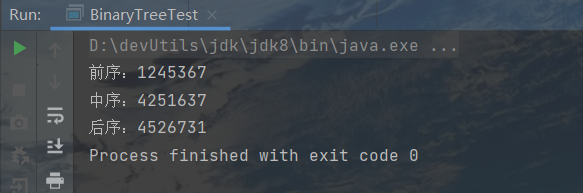
搞完了，一起来测试一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
package com.banmoon.datastructure;

public class BinaryTreeTest {

    public static void main(String[] args) {
        // 创建一个空树
        BinaryTree tree = new BinaryTree();
        // 创建根节点
        BinaryTree.TreeNode node = new BinaryTree.TreeNode(1);
        tree.setRoot(node);
        // 设置左节点
        BinaryTree.TreeNode leftNode = new BinaryTree.TreeNode(2);
        node.setLeftNode(leftNode);
        BinaryTree.TreeNode node4 = new BinaryTree.TreeNode(4);
        BinaryTree.TreeNode node5 = new BinaryTree.TreeNode(5);
        leftNode.setLeftNode(node4);
        leftNode.setRightNode(node5);
        // 设置右节点
        BinaryTree.TreeNode rightNode = new BinaryTree.TreeNode(3);
        node.setRightNode(rightNode);
        BinaryTree.TreeNode node6 = new BinaryTree.TreeNode(6);
        BinaryTree.TreeNode node7 = new BinaryTree.TreeNode(7);
        rightNode.setLeftNode(node6);
        rightNode.setRightNode(node7);

        System.out.print("前序：");
        tree.frontShow();
        System.out.println();
        System.out.print("中序：");
        tree.middleShow();
        System.out.println();
        System.out.print("后序：");
        tree.backShow();
    }
}

image-20220920153542125

1.3）是否包含

代码如下，篇幅有限，仅展示包含方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
@Data
@NoArgsConstructor
@AllArgsConstructor
public class BinaryTree {

    /**
     * 判断是否存在
     * @param value
     * @return
     */
    public boolean contains(Integer value) {
        return Objects.nonNull(value) && root.contains(value);
    }

    @Data
    @NoArgsConstructor
    public static class TreeNode {

        /**
         * 判断是否存在
         * @param value
         * @return
         */
        public boolean contains(Integer value) {
            // 对比当前节点
            boolean result = Objects.equals(this.value, value);
            // 对比左节点
            if (!result && Objects.nonNull(this.leftNode))
                result = this.leftNode.contains(value);
            // 对比右节点
            if (!result && Objects.nonNull(this.rightNode))
                result = this.rightNode.contains(value);
            return result;
        }
    }

}

此处的是否包含使用的前序遍历的方式进行判断，举一反三，中序遍历和后续遍历的判断相信也马上可以写出来。

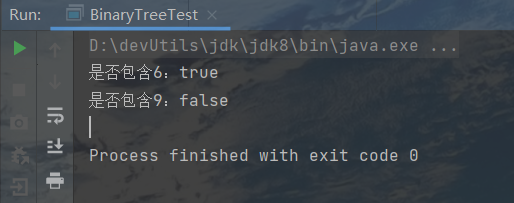
测试一下，判断树中是否存在6和9

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
package com.banmoon.datastructure;

public class BinaryTreeTest {

    public static void main(String[] args) {
        // 创建一个空树
        BinaryTree tree = new BinaryTree();
        // 创建根节点
        BinaryTree.TreeNode node = new BinaryTree.TreeNode(1);
        tree.setRoot(node);
        // 设置左节点
        BinaryTree.TreeNode leftNode = new BinaryTree.TreeNode(2);
        node.setLeftNode(leftNode);
        BinaryTree.TreeNode node4 = new BinaryTree.TreeNode(4);
        BinaryTree.TreeNode node5 = new BinaryTree.TreeNode(5);
        leftNode.setLeftNode(node4);
        leftNode.setRightNode(node5);
        // 设置右节点
        BinaryTree.TreeNode rightNode = new BinaryTree.TreeNode(3);
        node.setRightNode(rightNode);
        BinaryTree.TreeNode node6 = new BinaryTree.TreeNode(6);
        BinaryTree.TreeNode node7 = new BinaryTree.TreeNode(7);
        rightNode.setLeftNode(node6);
        rightNode.setRightNode(node7);

        System.out.println("是否包含6：" + tree.contains(6));
        System.out.println("是否包含9：" + tree.contains(9));
    }
}

image-20220921201319253

1.4）删除节点

删除节点时有这么一种情况，当删除了枝节点时，要不要将其子节点也一并删除掉。这一次就只需要将其一并删除，后面会有新类型的二叉树，保证仅删除指定的节点。

找到这个节点，让其父节点指向其的指针设置为null即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
@Data
@NoArgsConstructor
@AllArgsConstructor
public class BinaryTree {

    /**
     * 删除
     * @param value
     */
    public TreeNode delete(int value) {
        TreeNode node = root;
        if (root==null || value==root.value) {
            root = null;
        } else {
            node = root.delete(value);
        }
        return node;
    }

    @Data
    @NoArgsConstructor
    public static class TreeNode {

        /**
         * 删除
         * @param value
         * @return
         */
        public TreeNode delete(Integer value) {
            TreeNode node = null;
            if (Objects.nonNull(this.leftNode) && Objects.equals(this.leftNode.value, value)) {
                node = this.leftNode;
                this.leftNode = null;
                return node;
            }
            if (Objects.nonNull(this.rightNode) && Objects.equals(this.rightNode.value, value)) {
                node = this.rightNode;
                this.rightNode = null;
                return node;
            }
            if (Objects.nonNull(this.leftNode))
                node = this.leftNode.delete(value);
            if (node!=null && Objects.nonNull(this.rightNode))
                node = this.rightNode.delete(value);
            return node;
        }
    }

}

进行删除测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
package com.banmoon.datastructure;

public class BinaryTreeTest {

    public static void main(String[] args) {
        // 创建一个空树
        BinaryTree tree = new BinaryTree();
        // 创建根节点
        BinaryTree.TreeNode node = new BinaryTree.TreeNode(1);
        tree.setRoot(node);
        // 设置左节点
        BinaryTree.TreeNode leftNode = new BinaryTree.TreeNode(2);
        node.setLeftNode(leftNode);
        BinaryTree.TreeNode node4 = new BinaryTree.TreeNode(4);
        BinaryTree.TreeNode node5 = new BinaryTree.TreeNode(5);
        leftNode.setLeftNode(node4);
        leftNode.setRightNode(node5);
        // 设置右节点
        BinaryTree.TreeNode rightNode = new BinaryTree.TreeNode(3);
        node.setRightNode(rightNode);
        BinaryTree.TreeNode node6 = new BinaryTree.TreeNode(6);
        BinaryTree.TreeNode node7 = new BinaryTree.TreeNode(7);
        rightNode.setLeftNode(node6);
        rightNode.setRightNode(node7);

        tree.delete(2);
        tree.frontShow();
    }
}

image-20220922230137368

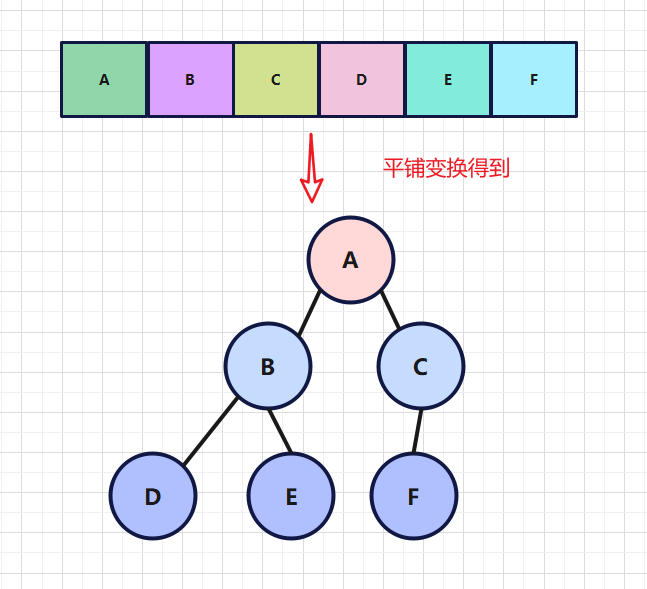
2）顺序存储的二叉树

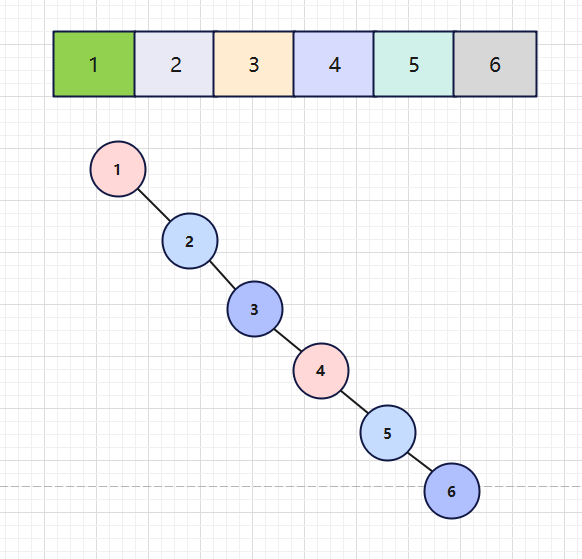
对于任何一段数组，我们都可以将其转为一个完全二叉树，平铺即可，如下

对于第n个元素来说，

  • 它的左子节点是：2n+12n+1

  • 它的右子节点是：2n+22n+2

  • 它的父节点是：n−12\frac{n-1}{2}

那么就好说了，代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
package com.banmoon.datastructure.ArrayBinaryTree;

import lombok.AllArgsConstructor;
import lombok.Data;

import java.util.Objects;

@Data
@AllArgsConstructor
public class ArrayBinaryTree {

    private Integer[] data;

    public void frontShow() {
        if (Objects.isNull(data) || data.length == 0)
            return;
        frontShow(0);
    }

    /**
     * 前序遍历
     * @param index
     */
    public void frontShow(int index) {
        System.out.println(data[index] + ",");
        int i;
        if ((i = index*2+1) < data.length)
            frontShow(i);
        if ((i = index*2+2) < data.length)
            frontShow(i);
    }
}

其他的都好说，看数据结构的需要，再进行添加，此处就不再添加了，仅作为了解。

作为常用的排序算法之一的堆排序，就是使用了此数据结构，相关传送门，了解堆排序如何进行排序的。

3）线索二叉树

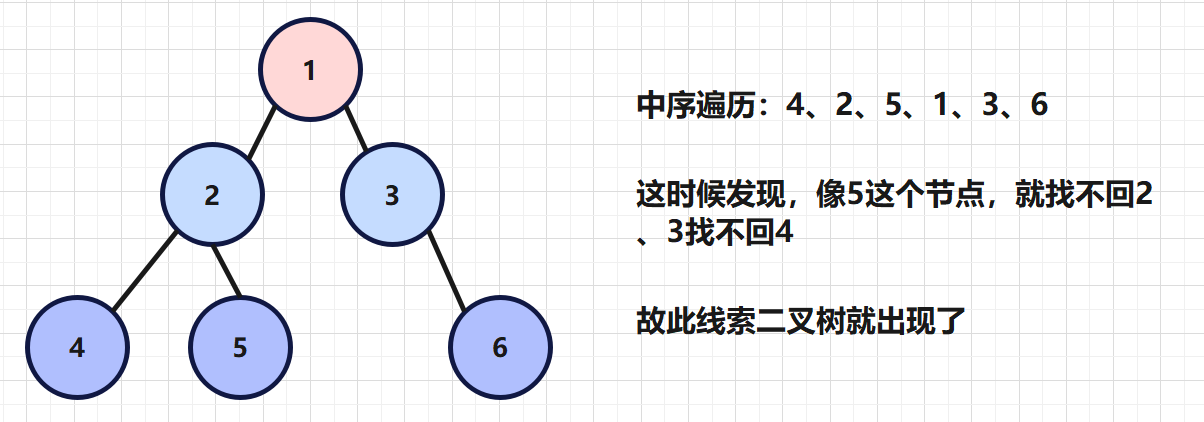
在寻常的二叉树遍历中，我们会发现这样一个问题，我们只能按照特定的顺序进行遍历，而不能从子节点返回到父节点。

如下图的中序遍历

image-20220930093216570

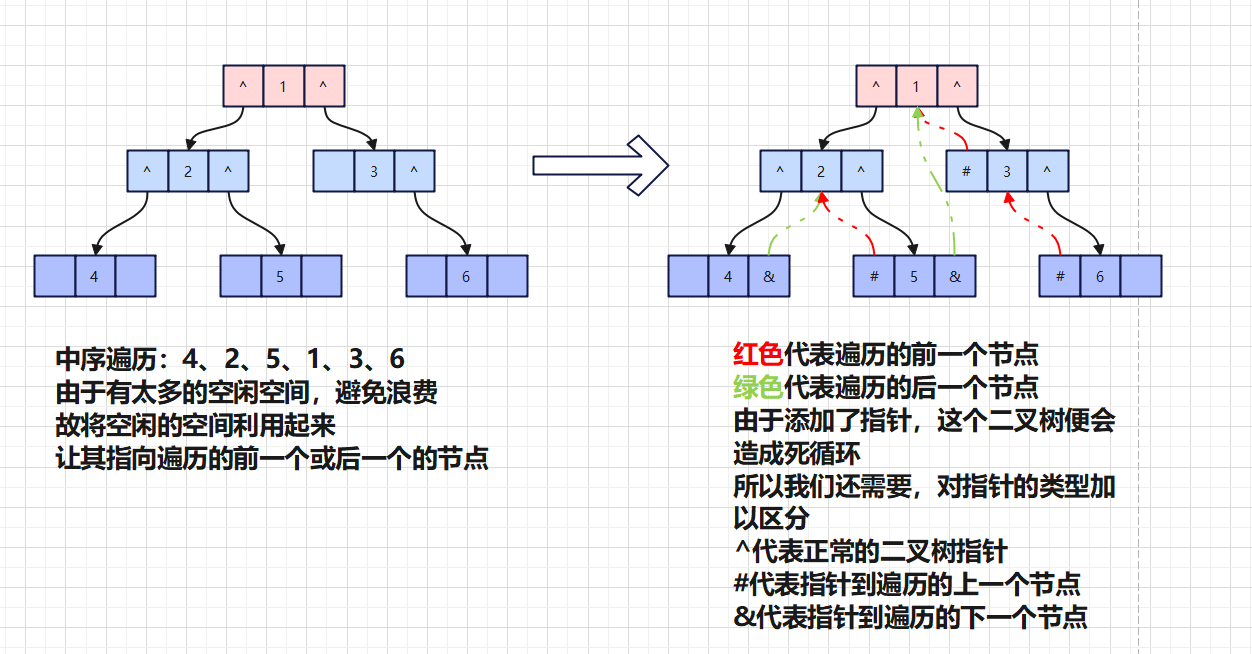
在一些节点中，4节点、5节点、3节点、6节点都有些指针空间的浪费，如下图进行改造

image-20221002182944893

如上图所示，原本空闲的空间瞬间就变得忙碌起来，这种过程叫做二叉树的线索化，这颗二叉树就便称为线索二叉树。

线索二叉树的线索化，与它的遍历方式有关，上述图例只是中序线索二叉树。

在线索二叉树中，一个节点的前一个节点，叫做前驱节点，后一个节点被称为后继节点。

那么这个，线索二叉树的编码是怎么样的呢，如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
package com.banmoon.datastructure;

import lombok.AllArgsConstructor;
import lombok.Data;
import lombok.NoArgsConstructor;

import java.util.Objects;

/**
 * 线索二叉树
 */
@Data
@NoArgsConstructor
@AllArgsConstructor
public class ThreadBinaryTree {

    /**
     * 根节点
     */
    private ThreadTreeNode root;

    /**
     * 临时存储前驱节点
     */
    private ThreadTreeNode preNode = null;

    public ThreadBinaryTree(Integer value) {
        this.root = new ThreadTreeNode(value);
    }

    /**
     * 线索化
     */
    public void thread() {
        thread(root);
    }

    /**
     * 线索化
     */
    public void thread(ThreadTreeNode node) {
        if (Objects.isNull(node))
            return;
        // 线索化左节点
        thread(node.leftNode);
        // 处理当前节点的前驱节点
        if (node.leftNode == null) {
            node.leftNode = preNode;
            node.leftNodeType = 1;
        }
        // 处理前驱节点的后继节点
        if (Objects.nonNull(preNode) && Objects.isNull(preNode.rightNode)) {
            preNode.rightNode = node;
            preNode.rightNodeType = 1;
        }
        preNode = node;
        // 序列化右节点
        thread(node.rightNode);
    }

    @Data
    @NoArgsConstructor
    public static class ThreadTreeNode {

        /**
         * 节点值
         */
        private Integer value;

        /**
         * 左节点
         */
        private ThreadTreeNode leftNode;

        /**
         * 右节点
         */
        private ThreadTreeNode rightNode;

        /**
         * 左节点类型，0=子节点，1=前驱节点
         */
        private short leftNodeType;

        /**
         * 左节点类型，0=子节点，1=后继节点
         */
        private short rightNodeType;

        public ThreadTreeNode(Integer value) {
            this.value = value;
        }
    }
}

4）赫夫曼树

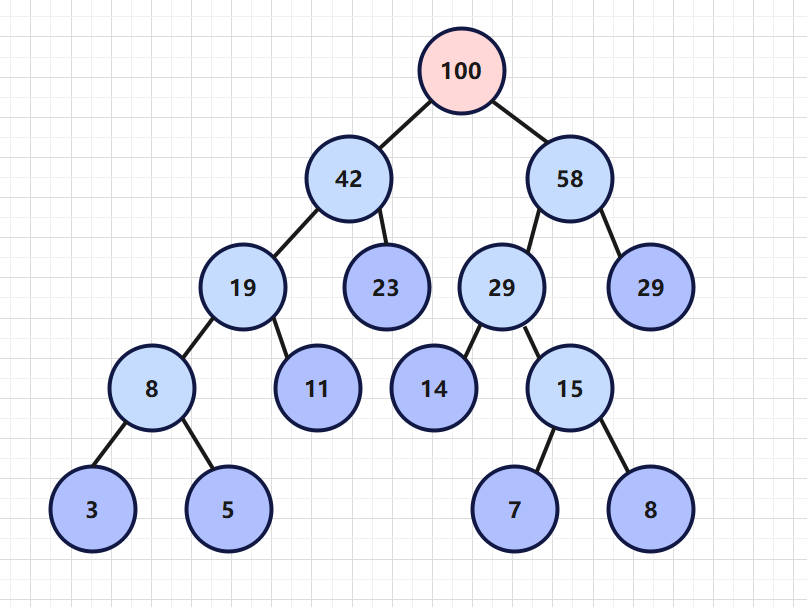
给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，这棵树就称为赫夫曼树，又称为最优二叉树。

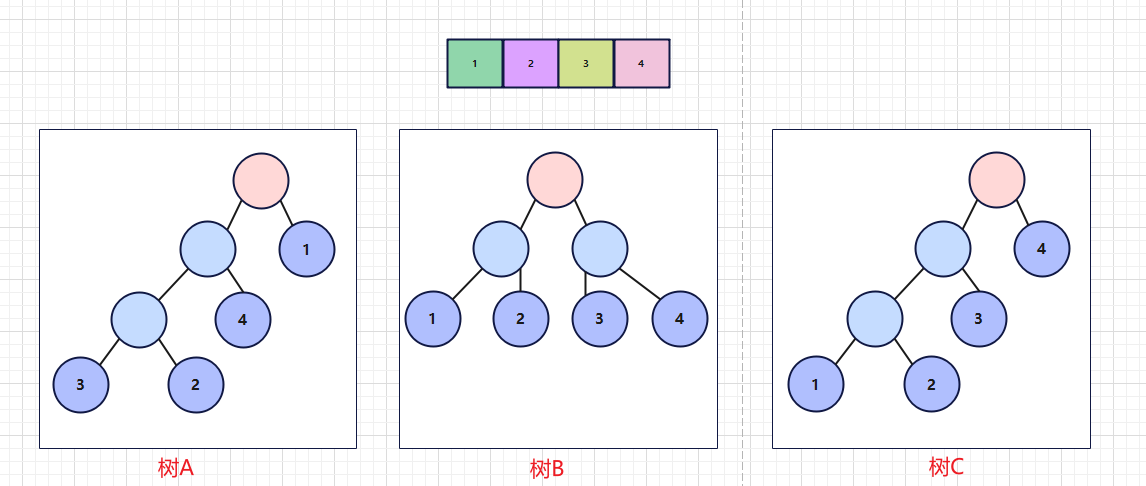
查看以下这几个数值，将们放入叶子节点中，我们可以摆出很多种不同的二叉树，分别计算数的带权路径。

image-20221005152653431

所谓带权路径，就是每个叶子节点上的权值与其经过的路径数乘积的和。有点抽象，看下面的计算方式

  • 树A：(1∗1)+(2∗4)+(3∗3)+(3∗2)=1+8+9+6=24(1*1)+(2*4)+(3*3)+(3*2)=1+8+9+6=24

  • 树B：(2∗1)+(2∗4)+(2∗3)+(2∗2)=2+8+5+4=19(2*1)+(2*4)+(2*3)+(2*2)=2+8+5+4=19

  • 树C：(1∗4)+(2∗3)+(3∗1)+(3∗2)=4+6+3+6=19(1*4)+(2*3)+(3*1)+(3*2)=4+6+3+6=19

明白了吗，简单的来说，就是将叶子节点与路径数相乘后，再相加。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
package com.banmoon.datastructure.HuffmanTree;

import lombok.AllArgsConstructor;
import lombok.Data;
import lombok.NoArgsConstructor;

import java.util.Arrays;
import java.util.Comparator;
import java.util.List;
import java.util.Objects;
import java.util.stream.Collectors;

@AllArgsConstructor
public class HuffmanTree {

    private Node root;

    public static HuffmanTree generateHuffmanTree(int[] arr) {
        return generateHuffmanTree(Arrays.stream(arr).boxed().toArray(Integer[]::new));
    }

    public static HuffmanTree generateHuffmanTree(Integer[] arr) {
        // 先进行转换
        List<Node> list = Arrays.stream(arr).map(value -> new Node(value)).collect(Collectors.toList());
        // 循环进行
        while (list.size() > 1) {
            // 排序
            list.sort(Comparator.comparingInt(Node::getValue));
            // 取出权值最小的两个节点
            Node left = list.get(0);
            Node right = list.get(1);
            // 创建一个新的节点，作为子树的根节点
            Node parent = new Node(left.getValue() + right.getValue());
            parent.setLeftNode(left);
            parent.setRightNode(right);
            // 将根节点加入数组，删除掉最小的两个节点
            list.remove(left);
            list.remove(right);
            list.add(parent);
        }
        return new HuffmanTree(list.get(0));
    }

    public void show() {
        if (Objects.nonNull(root))
            root.show();
    }
}

@Data
@NoArgsConstructor
class Node {
    private Integer value;
    private Node leftNode;
    private Node rightNode;

    public Node(Integer value) {
        this.value = value;
    }

    public void show() {
        if (Objects.nonNull(this.value))
            System.out.print(this.value + ",");
        if (Objects.nonNull(this.leftNode))
            this.leftNode.show();
        if (Objects.nonNull(this.rightNode))
            this.rightNode.show();
    }
}

创建赫夫曼数，也很简单，根据以下步骤来就可以

  1. 将数组其排序，升序进行排序

  2. 取出最小的两个数，组成一个子树，根节点的数值为他们的和

  3. 再将这颗树根节点的数值放入数组中，原本两个最小的数将从数组中移除

  4. 重复步骤1-3，直到最后数组中的数小于1

测试一下，如下进行测试

1
2
3
4
5
6
7
8
9
10
11
package com.banmoon.datastructure.HuffmanTree;

public class Test {

    public static void main(String[] args) {
        int[] arr = new int[]{3, 7, 8, 29, 5, 11, 23, 14};
        HuffmanTree huffmanTree = HuffmanTree.generateHuffmanTree(arr);
        huffmanTree.show();
    }

}

image-20221005171428539

按照前序遍历来看，确实是最优二叉树

image-20221005172446054

5）二叉查找树

二叉查找树，又名二叉排序树

定义：当一个二叉树，任意的非叶子节点，它的左节点比当前节点的值要小，并且它的右节点比当前节点的值要大，那么这个二叉树就可以被称为二叉查找树

二叉查找树的优点在于，他充分吸收了链表和数组结构带来的优劣势，对两者优缺点做出的一个折中的方案。

  • 数组：查询快，但插入和删除元素比较麻烦

  • 链表：插入删除元素快，但遍历查找比较麻烦

二叉查找树的话，使用的一个二分法对其进行折中，从而得到两者的好处，避免了上述问题极端的缺点。

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
package com.banmoon.datastructure.BinarySearchTree;

import lombok.Data;
import lombok.NoArgsConstructor;

import java.util.Arrays;
import java.util.Objects;
import java.util.Optional;

public class BinarySearchTree {

    private Node root;

    /**
     * 生成二叉查找树
     * @param values
     * @return
     */
    public static BinarySearchTree generate(int[] values) {
        BinarySearchTree binarySearchTree = new BinarySearchTree();
        Arrays.stream(values).forEach(binarySearchTree::add);
        return binarySearchTree;
    }

    /**
     * 添加节点
     * @param value
     */
    public void add(int value) {
        if (Objects.isNull(root))
            this.root = new Node(value);
        else
            root.add(value);
    }

    /**
     * 中序遍历
     */
    public void show() {
        if (Objects.nonNull(this.root))
            this.root.show();
    }

    /**
     * 查找节点
     * @param value
     * @return
     */
    public Node search(int value) {
        if (Objects.isNull(this.root))
            return null;
        return root.search(value);
    }

    /**
     * 删除节点
     * @param value
     * @return
     */
    public Node delete(int value) {
        if (Objects.isNull(this.root))
            return null;
        return this.root.delete(this, value, null);
    }

    /**
     * 重新设置左节点或右节点的值
     * @param originNode
     * @param targetNode
     */
    public void setNode(Node parent, Node originNode, Node targetNode) {
        // 如果父节点是null，则说明是根节点
        if (parent == null)
            this.root = targetNode;
        else if (parent.getLeftNode() == originNode)
            parent.setLeftNode(targetNode);
        else if (parent.getRightNode() == originNode)
            parent.setRightNode(targetNode);
    }

}

@Data
@NoArgsConstructor
class Node {
    private int value;
    private Node leftNode;
    private Node rightNode;

    public Node(int value) {
        this.value = value;
    }

    public void add(int value) {
        if (value < this.value) {
            if (Objects.nonNull(this.leftNode))
                this.leftNode.add(value);
            else
                this.leftNode = new Node(value);
        } else {
            if (Objects.nonNull(this.rightNode))
                this.rightNode.add(value);
            else
                this.rightNode = new Node(value);
        }
    }

    public void show() {
        if (Objects.nonNull(this.leftNode))
            this.leftNode.show();
        System.out.print(this.value + ", ");
        if (Objects.nonNull(this.rightNode))
            this.rightNode.show();
    }

    public Node search(int value) {
        if (this.value == value)
            return this;
        else if (this.value > value && Objects.nonNull(this.leftNode))
            return this.leftNode.search(value);
        else if (this.value < value && Objects.nonNull(this.rightNode))
            return this.rightNode.search(value);
        return null;
    }

    @Override
    public String toString() {
        return "Node{" +
                "value=" + value +
                '}';
    }

    /**
     * 分为3种情况
     * 1、删除叶子节点
     * 2、删除仅有一个节点的父节点的情况
     * 3、删除两个节点的父节点的情况
     * @param tree 当前的二叉查找树
     * @param value 删除的值
     * @param parent 当前节点的父节点
     * @return
     */
    public Node delete(BinarySearchTree tree, int value, Node parent) {
        if (this.value == value) {
            // 叶子节点，左节点和右节点都为空
            if (Objects.isNull(this.leftNode) && Objects.isNull(this.rightNode)) {
                tree.setNode(parent, this, null);
            }
            // 内部节点，且左节点和右节点都存在，
            else if (Objects.nonNull(this.leftNode) && Objects.nonNull(this.rightNode)) {
                Node tempLeftNode = this.leftNode;
                Node tempRightNode = this.rightNode;
                // 删除右子树中，最小的节点
                Node minNode = this.rightNode.deleteMin(this);
                // 最小的节点，用于替换该节点
                tree.setNode(parent, this, minNode);
                minNode.setLeftNode(tempLeftNode==minNode ? null : tempLeftNode);
                minNode.setRightNode(tempRightNode==minNode ? null : tempRightNode);
            }
            // 内部节点，左节点或右节点仅有一个存在
            else {
                Node node = Optional.of(this.leftNode).orElse(this.rightNode);
                tree.setNode(parent, this, node);
            }
            return this;
        } else if (this.value > value && Objects.nonNull(this.leftNode)) {
            return this.leftNode.delete(tree, value, this);
        } else if (this.value < value && Objects.nonNull(this.rightNode)) {
            return this.rightNode.delete(tree, value, this);
        }
        return null;
    }

    /**
     * 删除最小的那个节点
     * @param parent 当前节点的父节点
     * @return
     */
    private Node deleteMin(Node parent) {
        if (Objects.nonNull(this.leftNode)) {
            return this.leftNode.deleteMin(this);
        } else {
            parent.setLeftNode(this.rightNode);
        }
        return this;
    }

}

测试一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
package com.banmoon.datastructure.BinarySearchTree;

public class Test {

    public static void main(String[] args) {
        int[] values = {7, 3, 10, 12, 5, 1, 9};
        BinarySearchTree binarySearchTree = BinarySearchTree.generate(values);
        // 中序遍历
        binarySearchTree.show();
        // 查找节点
        Node node12 = binarySearchTree.search(12);
        Node node23 = binarySearchTree.search(23);
        System.out.println(System.lineSeparator() + node12);
        System.out.println(node23);
        // 删除节点
        System.out.println(System.lineSeparator() + "======== 分割线 ========");
        binarySearchTree.delete(12);
        binarySearchTree.show();
        System.out.println(System.lineSeparator() + "======== 分割线 ========");
        binarySearchTree.delete(7);
        binarySearchTree.show();
        System.out.println(System.lineSeparator() + "======== 分割线 ========");
        binarySearchTree.delete(9);
        binarySearchTree.show();
        System.out.println(System.lineSeparator() + "======== 分割线 ========");
        binarySearchTree.delete(10);
        binarySearchTree.show();
        System.out.println();
    }
}

image-20221006195118388

6）平衡二叉树

在了解平衡二叉树之前，我们先得看看上一章的二叉查找树有什么问题。如下图

image-20221006201057430

也就是说，二叉查找树，在某一时刻，会退化成为链表。

而为了针对这个问题，平衡二叉树就出现了，它就是为了解决二叉查找树左右子树高度相差太大带来的一个极端链表化的一个问题。

对于平衡二叉树，定义是，对于任何一个节点，它的左子树与右子树的高度差都不能大于1，故此我们需要将二叉查找树，做一些优化。

如果要编码，我们需要一些基本的方法，比如说当前树的高度，左子树的高度，右子树的高度，当前树的高度差等等基础方法。再加上原来二叉查找树就有的插入方法，本章也仅仅只考虑插入方法，删除方法就只是逆着来的。

对于高度，有下面几点的参考

  • 当左子树的高度比右子树的要大许多，那么整体需要进行右旋转

  • 当右子树的高度比左子树的要大许多，那么整体需要进行左旋转

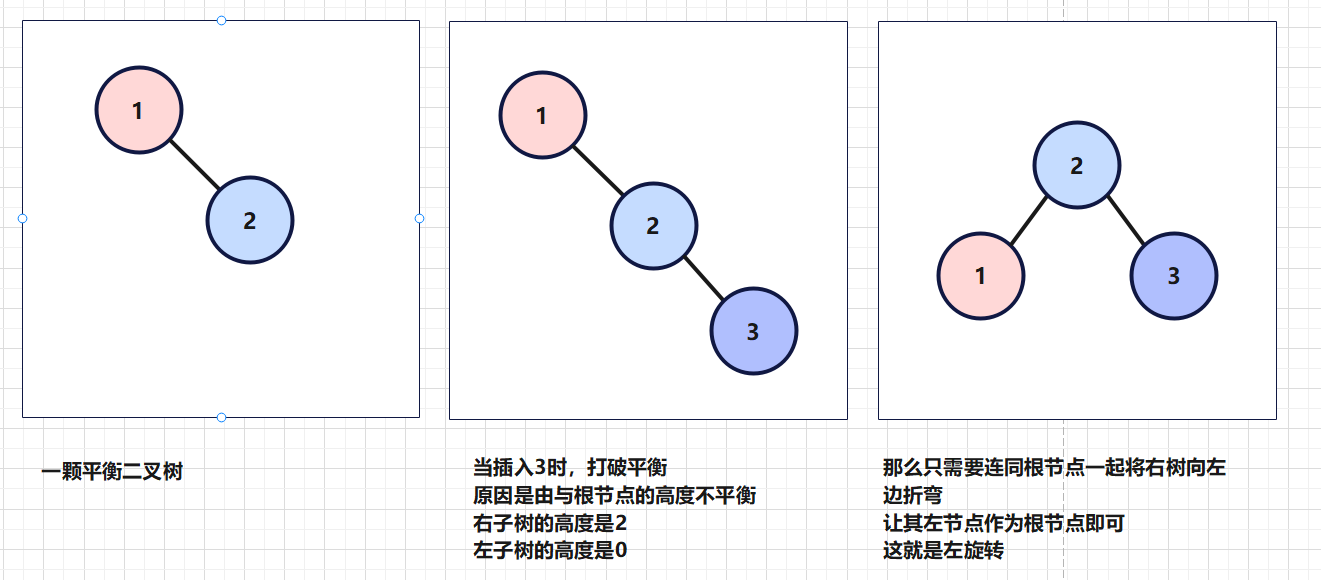
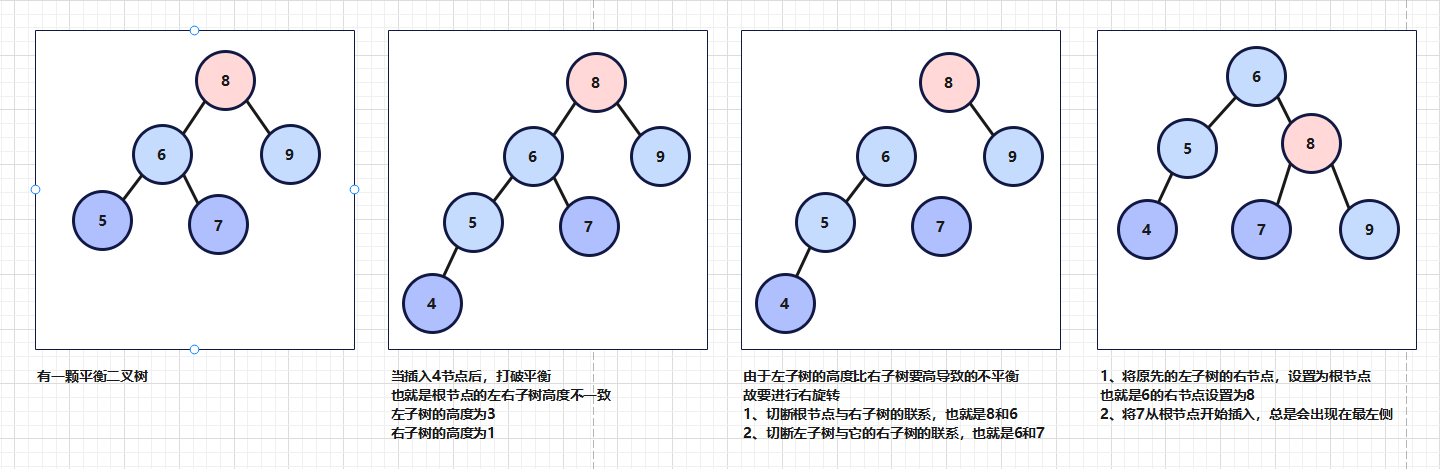
可以这么想，哪边的数要是比另一边要高（大于1），那么这棵树就要向右边折弯，这便是单旋转。如下图

左旋转 image-20221007143446811
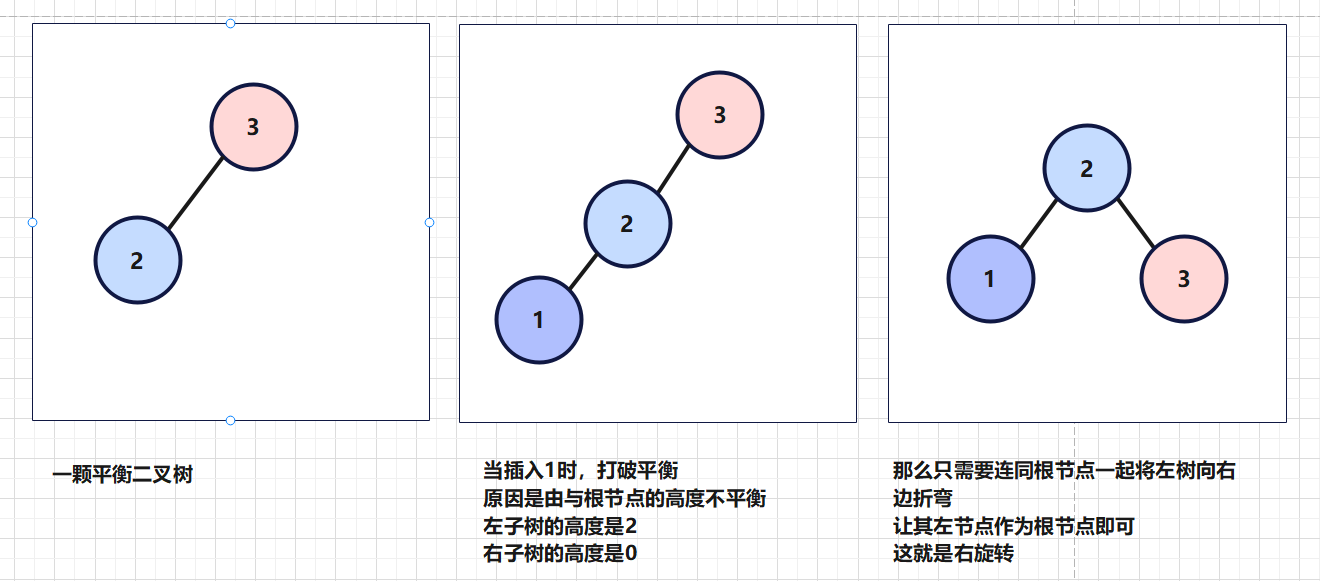
右旋转 image-20221007143525466

上面只是基础的单旋转，比较简单，这时候我们将对子节点进行复杂化，要是万一，子节点还有子节点呢。如下图

image-20221007151921572

思考一下，为什么在进行右旋转，取到左节点的右子树，在进行插入的时候，总是会出现在当前子树的最左侧呢？

如上图，7在插入到8这颗子树的时候，为什么跑到了左节点的位置

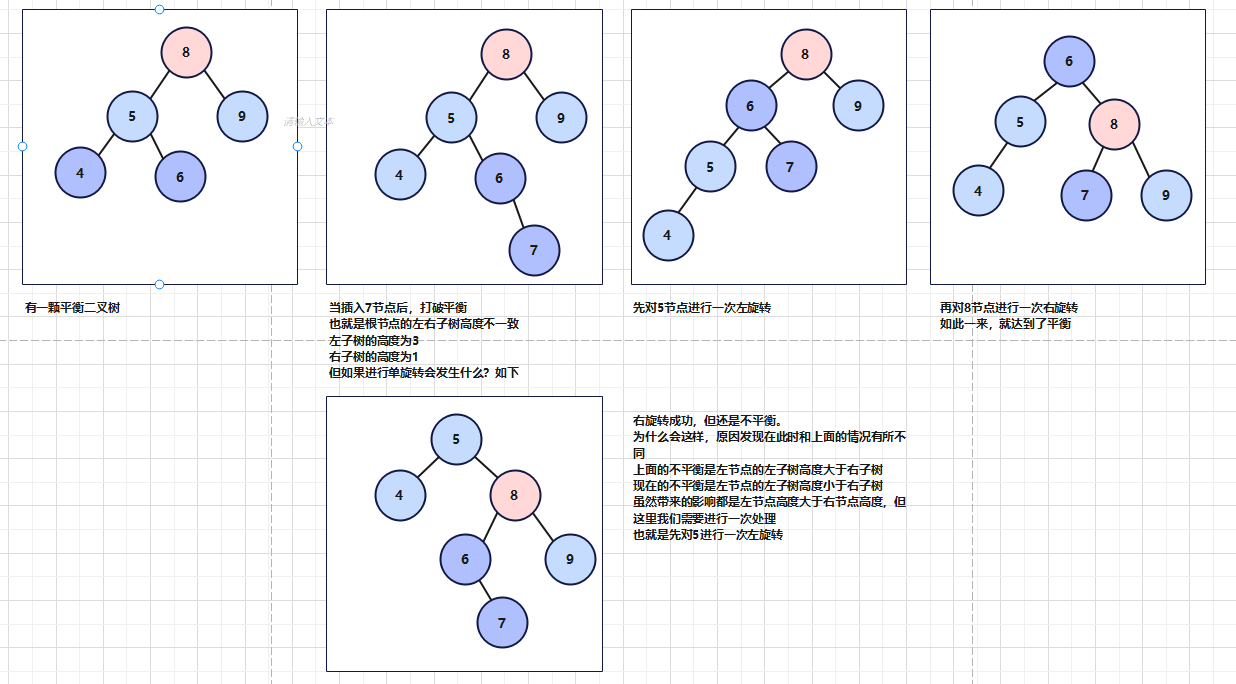
上述情况适用于单旋转的情况，那么还有一种可能，如下图

image-20221007153928839

那么代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
package com.banmoon.datastructure.BalanceBinaryTree;

import lombok.Data;
import lombok.NoArgsConstructor;

import java.util.Arrays;
import java.util.Objects;

@Data
public class BalanceBinaryTree {

    private Node root;

    /**
     * 添加节点
     * @param value
     */
    public void add(int value) {
        if (Objects.isNull(root))
            this.root = new Node(value);
        else
            root.add(new Node(value), this, null);
    }

    /**
     * 生成二叉查找树
     * @param values
     * @return
     */
    public static BalanceBinaryTree generate(int[] values) {
        BalanceBinaryTree binarySearchTree = new BalanceBinaryTree();
        Arrays.stream(values).forEach(binarySearchTree::add);
        return binarySearchTree;
    }

    /**
     * 中序遍历
     */
    public void show() {
        if (Objects.nonNull(this.root))
            this.root.show();
    }

    public boolean isBalance() {
        if (Objects.isNull(this.root))
            return true;
        return Math.abs(this.root.heightDifference()) <= 1;
    }

}

@Data
@NoArgsConstructor
class Node {
    private int value;
    private Node leftNode;
    private Node rightNode;

    public Node(int value) {
        this.value = value;
    }

    public void add(Node node, BalanceBinaryTree tree, Node parent) {
        if(Objects.isNull(node))
            return;
        if (node.getValue() < this.value) {
            if (Objects.nonNull(this.leftNode))
                this.leftNode.add(node, tree, this);
            else
                this.leftNode = node;
        } else {
            if (Objects.nonNull(this.rightNode))
                this.rightNode.add(node, tree, this);
            else
                this.rightNode = node;
        }
        // 检查是否平衡二叉树，此处说明左子树的高度比右子树要高，导致的不平衡，需要进行右旋转
        if (this.heightDifference() > 1) {
            // 如果左节点的左子树高度比其右子树的高度要小，就需要对其进行一次左旋转
            if (this.leftNode.leftHeight() < this.leftNode.rightHeight())
                this.leftNode.leftRotate(tree, this);
            this.rightRotate(tree, parent);
        }
        // 此处说明右子树的高度比左子树要高，需要进行左旋转
        else if (this.heightDifference() < -1) {
            // 如果右节点的左子树高度比其右子树的高度要大，就需要对其进行一次右旋转。避免整体左旋转后，高度不平衡
            if (this.rightNode.leftHeight() > this.rightNode.rightHeight())
                this.rightNode.rightRotate(tree, this);
            this.leftRotate(tree, parent);
        }
    }

    /**
     * 对当前节点进行右旋转
     */
    private void rightRotate(BalanceBinaryTree tree, Node parent) {
        // 取得当前节点的左节点
        Node tempLeftNode = this.leftNode;
        // 将当前节点的左节点置空
        this.leftNode = null;
        // 取得原先左节点的右节点，让其作为新的节点插入至当前节点的子树中
        this.add(tempLeftNode.rightNode, tree, parent);
        // 将原先左节点的右节点设置为当前节点
        tempLeftNode.rightNode = this;
        // 判断当前节点是否是根节点，将原先的左节点设置为根节点
        if (tree.getRoot() == this)
            tree.setRoot(tempLeftNode);
        // 父节点的右节点指向原先的左节点
        else
            parent.rightNode = tempLeftNode;
    }

    /**
     * 对当前节点进行左旋转
     */
    private void leftRotate(BalanceBinaryTree tree, Node parent) {
        // 取得当前节点的右节点
        Node tempRightNode = this.rightNode;
        // 将当前节点的右节点置空
        this.rightNode = null;
        // 取得原先右节点的左节点，让其作为新的节点插入至当前节点的子树中
        this.add(tempRightNode.leftNode, tree, parent);
        // 将原先右节点的左节点设置为当前节点
        tempRightNode.leftNode = this;
        // 判断当前节点是否是根节点，将原先的右节点设置为根节点
        if (tree.getRoot() == this)
            tree.setRoot(tempRightNode);
        // 父节点的左节点指向原先的右节点
        else
            parent.leftNode = tempRightNode;
    }

    /**
     * 高度差
     * @return
     */
    public int heightDifference() {
        return leftHeight() - rightHeight();
    }

    /**
     * 当前节点的高度
     * @return
     */
    public int height() {
        return Math.max(leftHeight(), rightHeight()) + 1;
    }

    /**
     * 左子树的高度
     * @return
     */
    public int leftHeight() {
        return Objects.isNull(this.leftNode)? 0 : this.leftNode.height();
    }

    /**
     * 左子树的高度
     * @return
     */
    public int rightHeight() {
        return Objects.isNull(this.rightNode)? 0 : this.rightNode.height();
    }

    public void show() {
        if (Objects.nonNull(this.leftNode))
            this.leftNode.show();
        System.out.print(this.value + ", ");
        if (Objects.nonNull(this.rightNode))
            this.rightNode.show();
    }
}

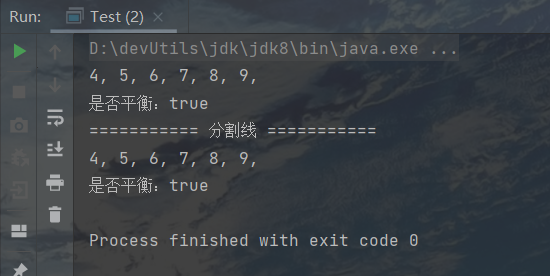
测试一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
package com.banmoon.datastructure.BalanceBinaryTree;

public class Test {

    public static void main(String[] args) {
        // 单旋转，右旋转
        int[] values = {8, 6, 9, 5, 7, 4};
        BalanceBinaryTree tree = BalanceBinaryTree.generate(values);
        // 中序遍历
        tree.show();
        // 是否平衡
        System.out.println("\n是否平衡：" + tree.isBalance());

        System.out.println("=========== 分割线 ===========");
        // 双旋转，先进行左旋转，再右旋转
        values = new int[]{8, 9, 5, 4, 6, 7};
        BalanceBinaryTree tree1 = BalanceBinaryTree.generate(values);
        tree1.show();
        System.out.println("\n是否平衡：" + tree1.isBalance());
    }
}

image-20221007154359718

四、最后

这个国庆，死磕二叉树，尤其是平衡二叉树，真的难，断断续续我理解了好久。

至于为什么会断断续续的，因为Lucy，意难平啊，emo了好久。

image-20221007155224523

我是半月，祝你幸福！！！